在讲解Breadth-first search 算法之前,我们先简单介绍两种数据类型Graph和Queue。
Graph
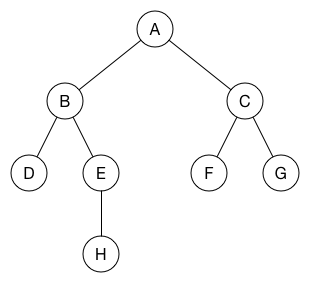
这就是一个图,它由两部分组成:
- 节点, 使用圆圈表示的部分
- 边, 使用线表示的地方,通常都是有方向的线
这种数据结构可以形象的表示一个网络,而在实际解决问题的时候,我们除了找到类似网络的模拟外,还需要考虑下边两点:
- 需要找到某条路径
- 需要找到到达某个节点的最短路径
而如何实现这个查找的过程就用到了算法。
在项目管理专业的工程方法中,存在一个有向连接图方法,根据这个图我们就可以划出邻接矩阵,然后再求出可达矩阵,缩减矩阵等等,说这些内容,是想表达在用代码模拟图的时候,可以使用矩阵的方式来描述,但本篇中采用的是另一种方式,我们使用数组保存某个节点的neighbor节点。
上边一段话会在下边的代码中进行展示:
Graph.swift// MARK: - Edgepublic class Edge: Equatable { public var neighbor: Node public init(neighbor: Node) { self.neighbor = neighbor }}public func == (lhs: Edge, rhs: Edge) -> Bool { return lhs.neighbor == rhs.neighbor}// MARK: - Nodepublic class Node: CustomStringConvertible, Equatable { public var neighbors: [Edge] public private(set) var label: String public var distance: Int? public var visited: Bool public init(label: String) { self.label = label neighbors = [] visited = false } public var description: String { if let distance = distance { return "Node(label: \(label), distance: \(distance))" } return "Node(label: \(label), distance: infinity)" } public var hasDistance: Bool { return distance != nil } public func remove(edge: Edge) { neighbors.remove(at: neighbors.index { $0 === edge }!) }}public func == (lhs: Node, rhs: Node) -> Bool { return lhs.label == rhs.label && lhs.neighbors == rhs.neighbors}// MARK: - Graphpublic class Graph: CustomStringConvertible, Equatable { public private(set) var nodes: [Node] public init() { self.nodes = [] } public func addNode(_ label: String) -> Node { let node = Node(label: label) nodes.append(node) return node } public func addEdge(_ source: Node, neighbor: Node) { let edge = Edge(neighbor: neighbor) source.neighbors.append(edge) } public var description: String { var description = "" for node in nodes { if !node.neighbors.isEmpty { description += "[node: \(node.label) edges: \(node.neighbors.map { $0.neighbor.label})]" } } return description } public func findNodeWithLabel(_ label: String) -> Node { return nodes.filter { $0.label == label }.first! } public func duplicate() -> Graph { let duplicated = Graph() for node in nodes { _ = duplicated.addNode(node.label) } for node in nodes { for edge in node.neighbors { let source = duplicated.findNodeWithLabel(node.label) let neighbour = duplicated.findNodeWithLabel(edge.neighbor.label) duplicated.addEdge(source, neighbor: neighbour) } } return duplicated }}public func == (lhs: Graph, rhs: Graph) -> Bool { return lhs.nodes == rhs.nodes} Queue
队列同样是一种数据结构,它遵循FIFO的原则,因为Swift没有现成的这个数据结构,因此我们手动实现一个。
值得指出的是,为了提高性能,我们针对在数组中读取数据做了优化。比如,当在数组中取出第一个值时,如果不做优化,那么这一步的消耗为O(n),我们采取的解决方法就是把该位置先置为nil,然后设置一个阈值,当达到阈值时,在对数组做进不去的处理。
这一部分的代码相当简单
Queue.swiftpublic struct Queue{ fileprivate var array = [T?]() fileprivate var head = 0 public init() { } public var isEmpty: Bool { return count == 0 } public var count: Int { return array.count - head } public mutating func enqueue(_ element: T) { array.append(element) } public mutating func dequeue() -> T? { guard head < array.count, let element = array[head] else { return nil } array[head] = nil head += 1 let percentage = Double(head) / Double(array.count) if array.count > 50 && percentage > 0.25 { array.removeFirst(head) head = 0 } return element } public var front: T? { if isEmpty { return nil } else { return array[head] } }}
Breadth-first search
其实这个算法的思想也很简单,我们已源点为中心,一层一层的往外查找,在遍历到某一层的某个节点时,如果该节点是我们要找的数据,那么就退出循环,如果没找到,那么就把该节点的neighbor节点加入到队列中,这就是该算法的核心原理。
打破循环的条件需要根据实际情况来设定。
//: Playground - noun: a place where people can playimport UIKitimport Foundationvar str = "Hello, playground"func breadthFirstSearch(_ graph: Graph, source: Node) -> [String] { /// 创建一个队列并把源Node放入这个队列中 var queue = Queue () queue.enqueue(source) /// 创建一个数组用于存放结果 var nodesResult = [source.label] /// 设置Node的visited为true,因为我们会把这个当做一个开关 source.visited = true /// 开始遍历 while let node = queue.dequeue() { for edge in node.neighbors { let neighborNode = edge.neighbor if !neighborNode.visited { queue.enqueue(neighborNode) neighborNode.visited = true nodesResult.append(neighborNode.label) } } } return nodesResult}let graph = Graph()let nodeA = graph.addNode("a")let nodeB = graph.addNode("b")let nodeC = graph.addNode("c")let nodeD = graph.addNode("d")let nodeE = graph.addNode("e")let nodeF = graph.addNode("f")let nodeG = graph.addNode("g")let nodeH = graph.addNode("h")graph.addEdge(nodeA, neighbor: nodeB)graph.addEdge(nodeA, neighbor: nodeC)graph.addEdge(nodeB, neighbor: nodeD)graph.addEdge(nodeB, neighbor: nodeE)graph.addEdge(nodeC, neighbor: nodeF)graph.addEdge(nodeC, neighbor: nodeG)graph.addEdge(nodeE, neighbor: nodeH)graph.addEdge(nodeE, neighbor: nodeF)graph.addEdge(nodeF, neighbor: nodeG)let nodesExplored = breadthFirstSearch(graph, source: nodeA)print(nodesExplored) 总结
实现的代码不是重点,重要的是理解这些思想,在实际情况中能够得出解决的方法。当然跟实现的语言也没有关系。
使用playground时,command + 1可以看到Source文件夹,把单独的类放进去就可以加载进来了。上边的内容来自这个网站